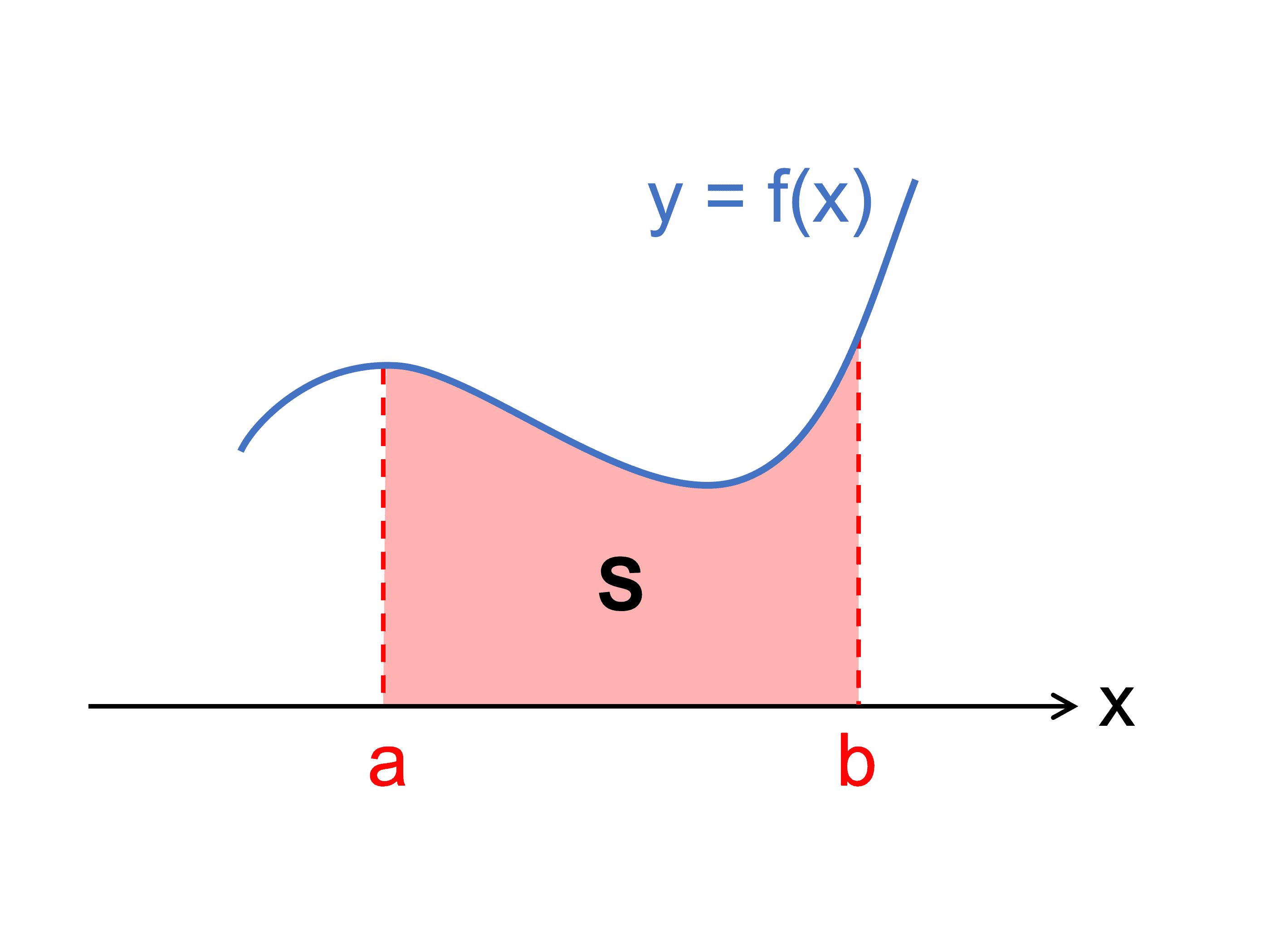
定積分で面積を求めるときの考え方は、これまでとまったく同じです。 上側の曲線と下側の曲線に注目 して、 「上の曲線－下の曲線」の積分 で求めるのでした。 今回の図をよく見てください。 交点の右と左でグラフの上下関係が変わっていますね。 交点の左側では、上がy=g (x)下がy=f (x) 交点の右側では、上がy=f (x)下がy=g (x)です。 この図形は2つに分断して考えましょう。 交点の左側 では、 上がy=g (x)下がy=f (x) で面積のスタートはx=a，終点はx=pです。 面積= ∫ ap {g (x)-f (x)}dx と求めることができますね! 交点の右側 では、 上がy=f (x)下がy=g (x) で面積のスタートはx=p，終点はx=bです。. y = x 2 − 2 x + 4 = ( x − 1) 2 + 3. はグラフを書くと. になりますね。 これは大丈夫なはず。 では例えば. この図にある斜線の部分の面積を求めることはできますか。 できそうにも思えますが二次関数は曲線なので求めたい面積の上の方が曲がっています。 ですから私たちは この面積を正確に求めることは今の時点で不可能 です。 ですが積分を知った私たちにはこれができます。 実はこの面積は. ∫ 1 2 x 2 − 2 x + 4 d x. という 定積分 によって正確に求めることができるのです。 欲しい 面積の両端の x 座標と積分を用いれば この面積を求めることができます。 そしてこの インテグラルに何やら数字がついた積分が「定積分」 です。

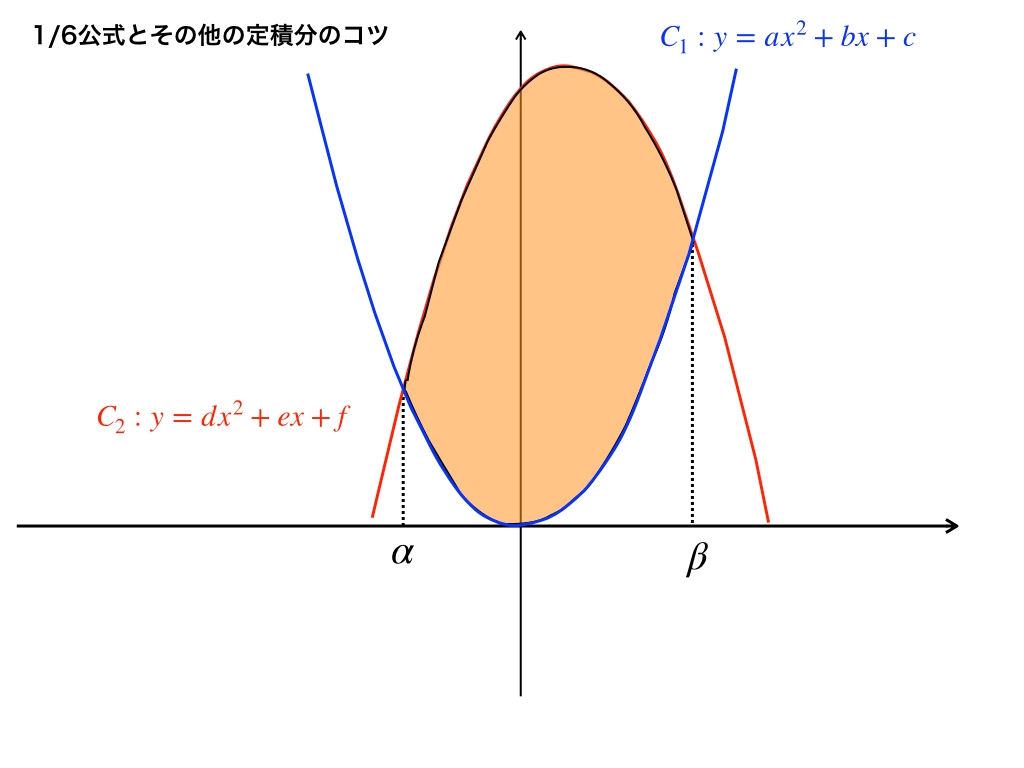
面積公式(6分の1等)をうまく使う方法を解説!数2積分法

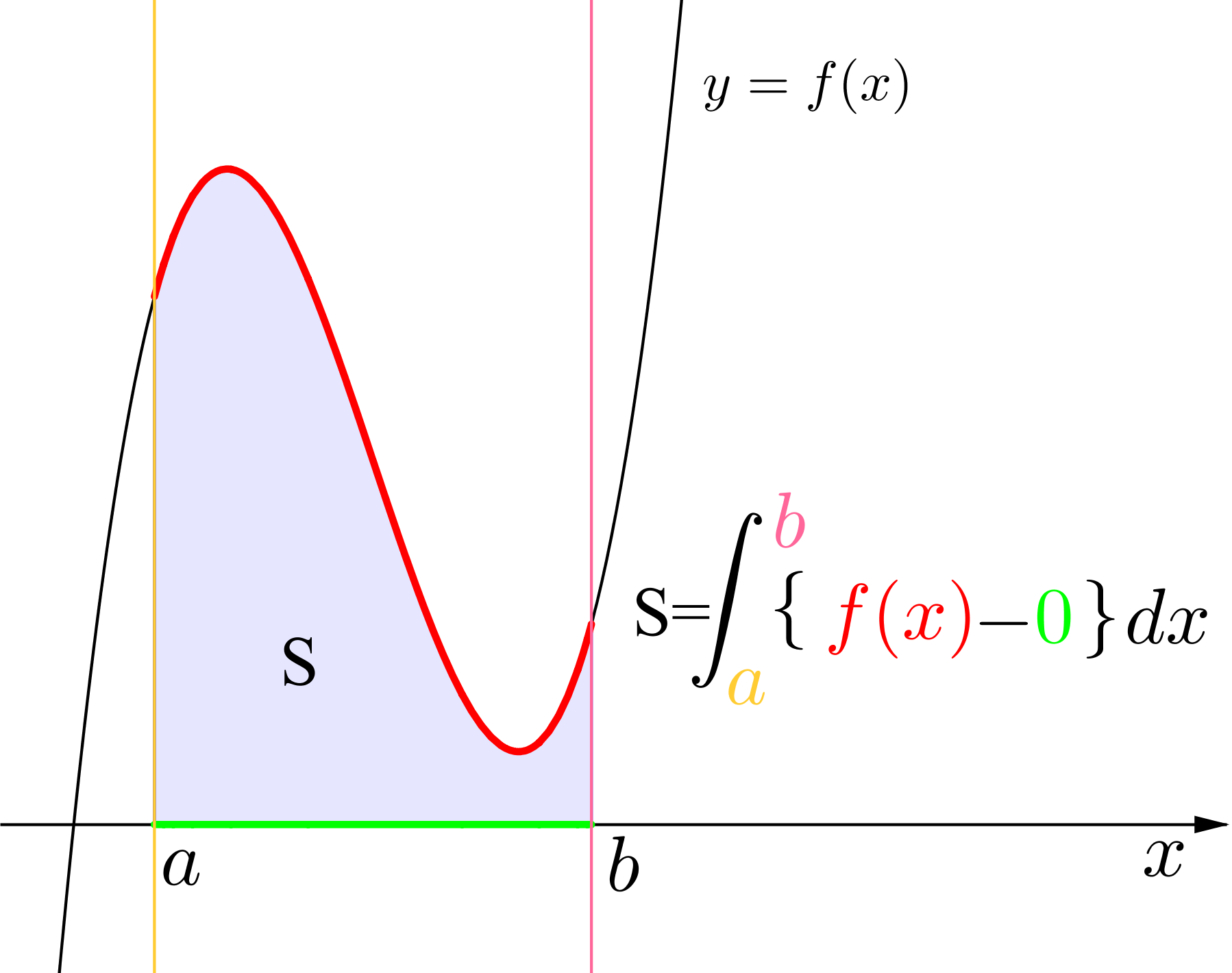
定積分と面積（基本）

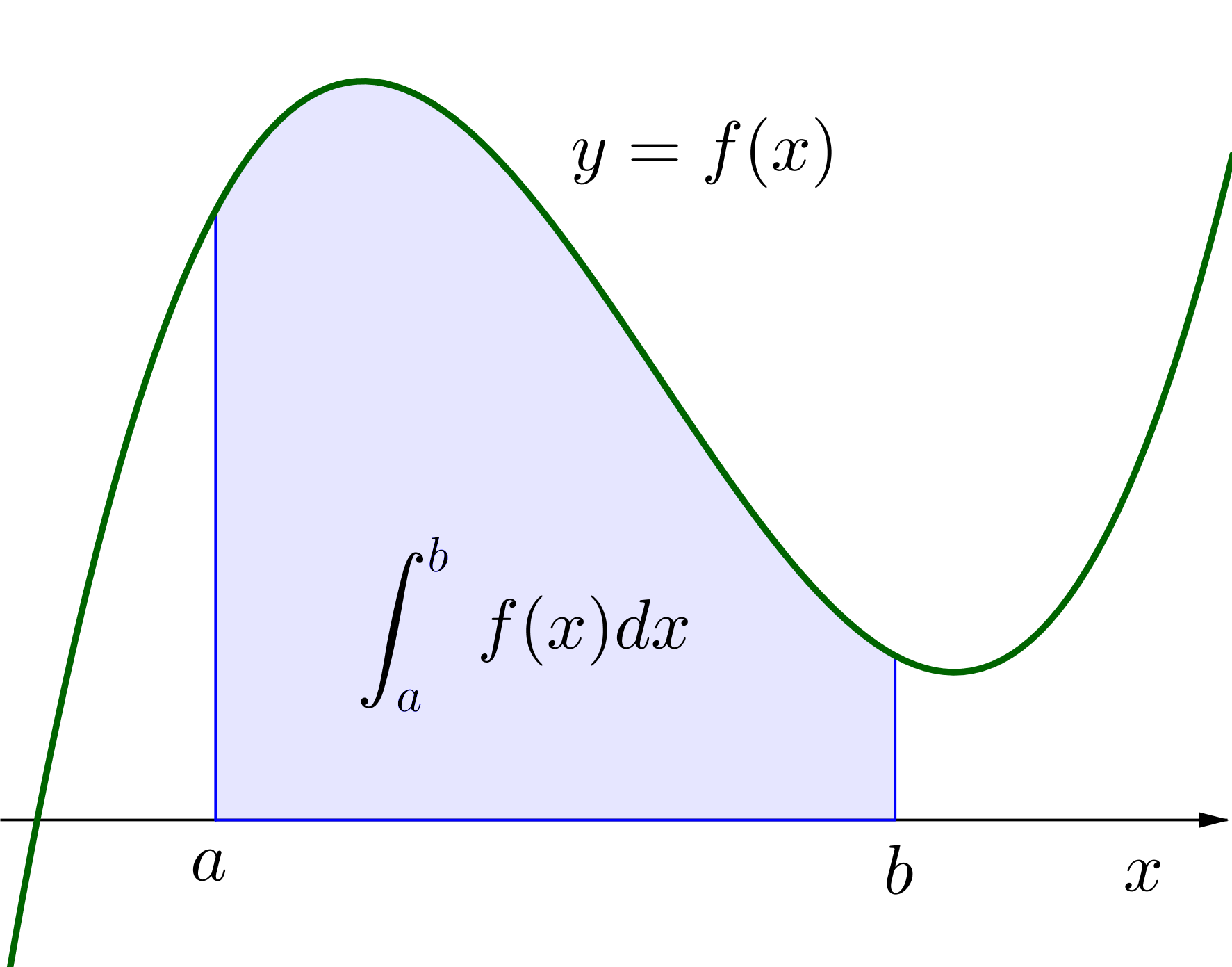
定積分の計算と定積分の表す面積

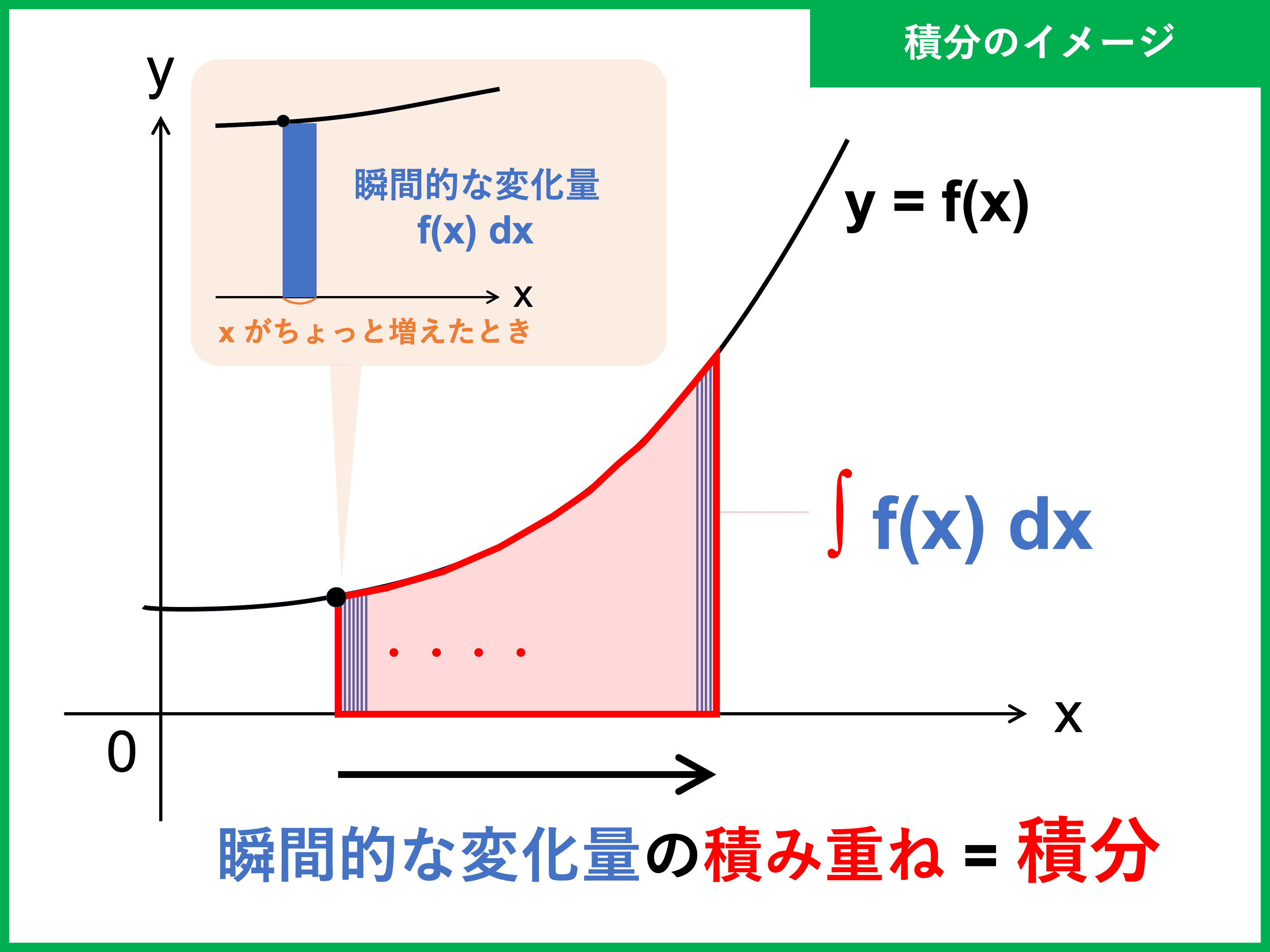
積分とは？公式や積分計算のやり方、積分定数の意味 受験辞典

定積分とは？計算・面積公式や求め方をわかりやすく解説！ 受験辞典

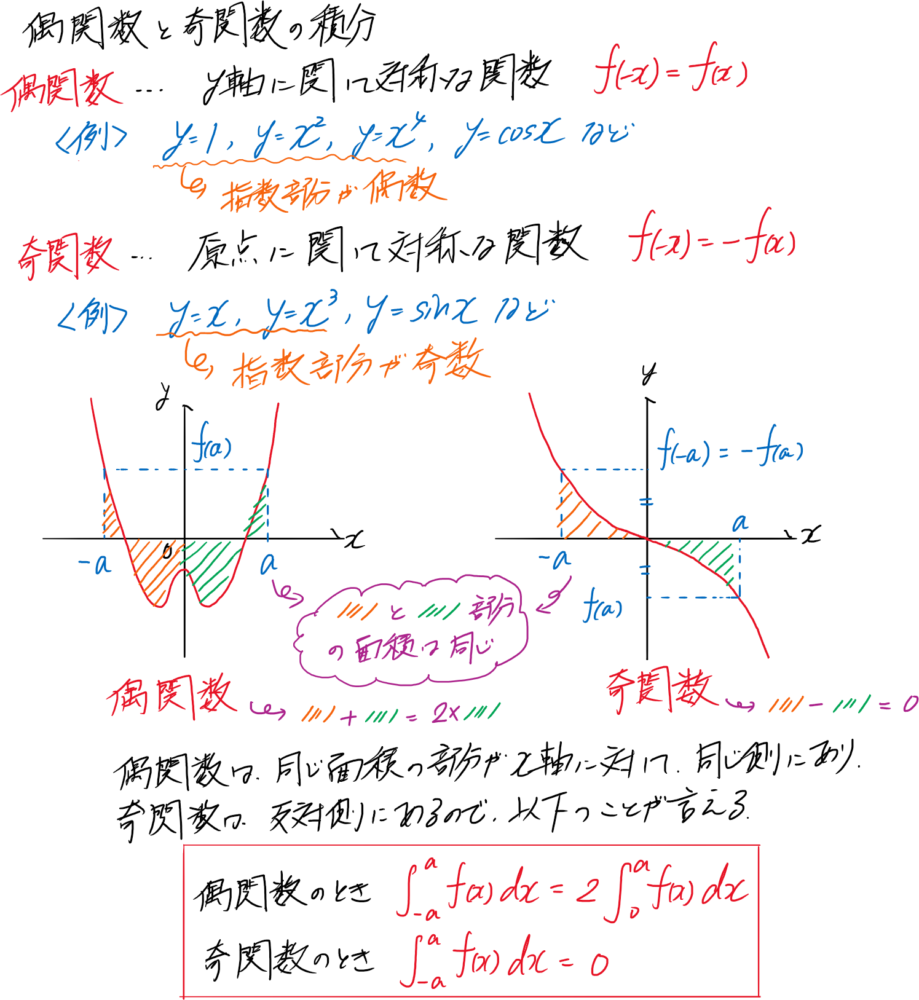
偶関数・奇関数の積分 ｜ 富岡市の総合学習塾 トータルアカデミー

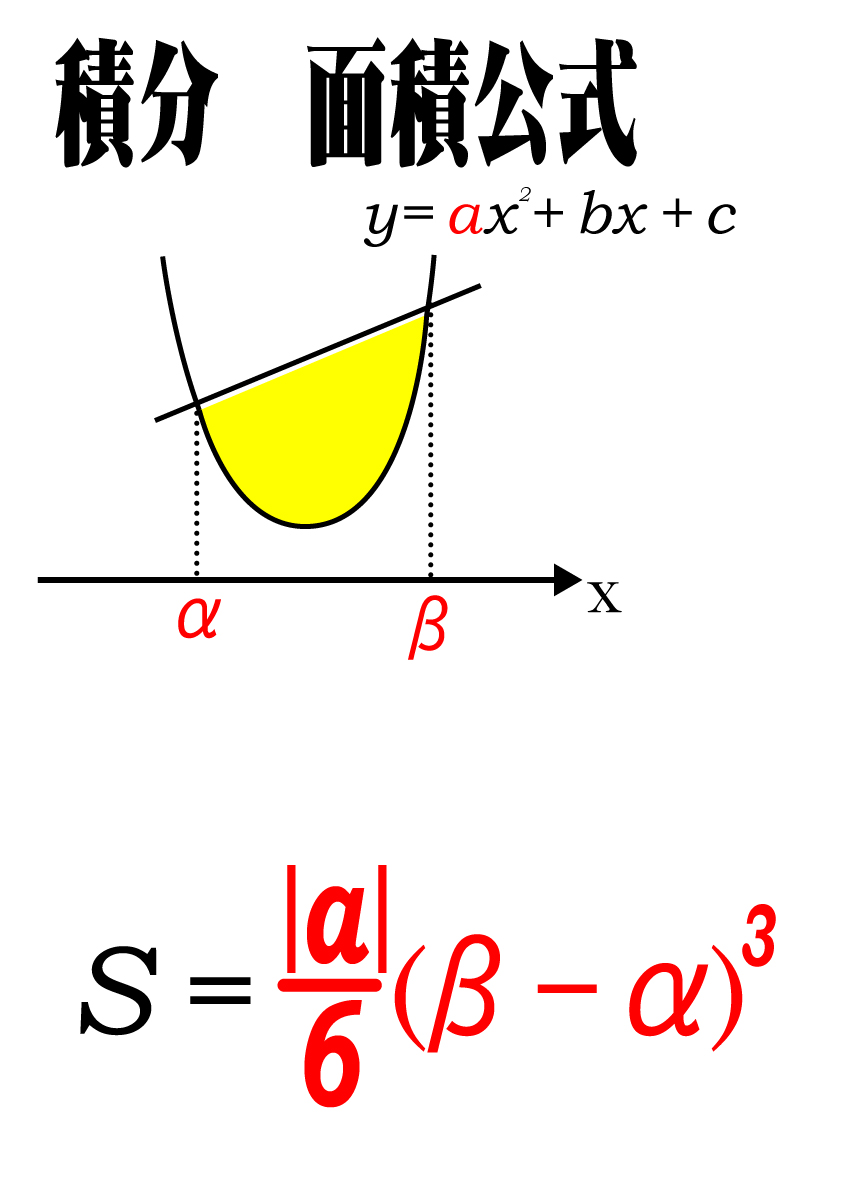
積分単元 面積公式① 時習館ゼミナール・高等部

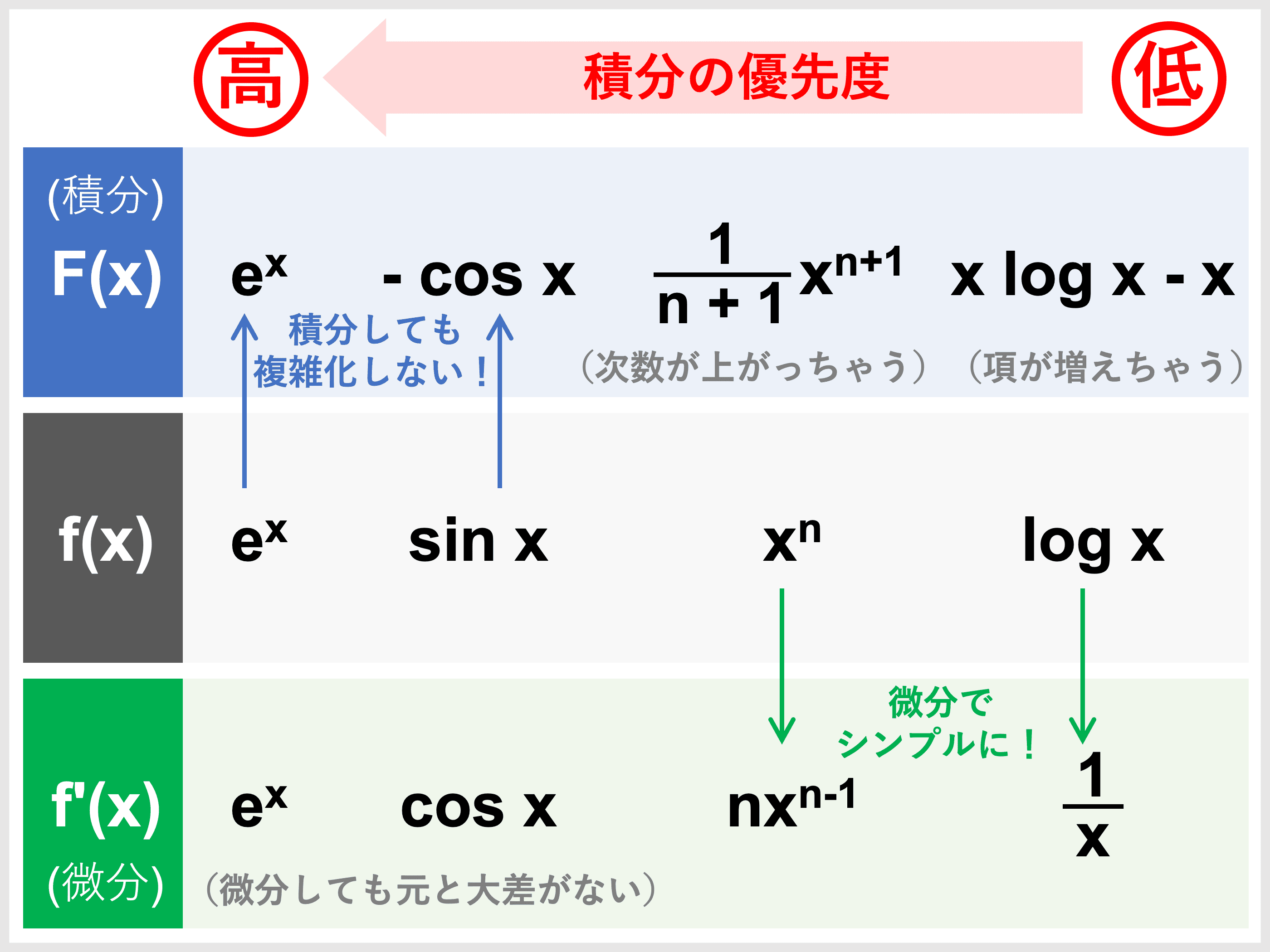
部分積分法の公式や証明、使うコツをわかりやすく解説！ 受験辞典

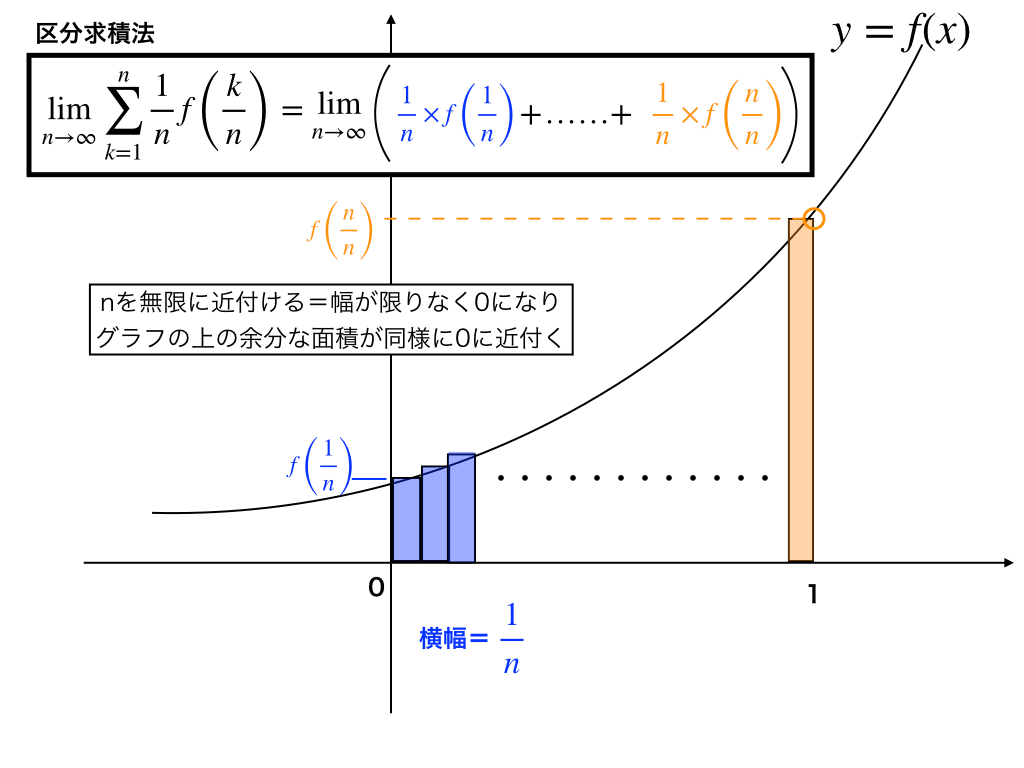
微分積分とは?高校数学の基礎から応用までわかりやすい記事総まとめ

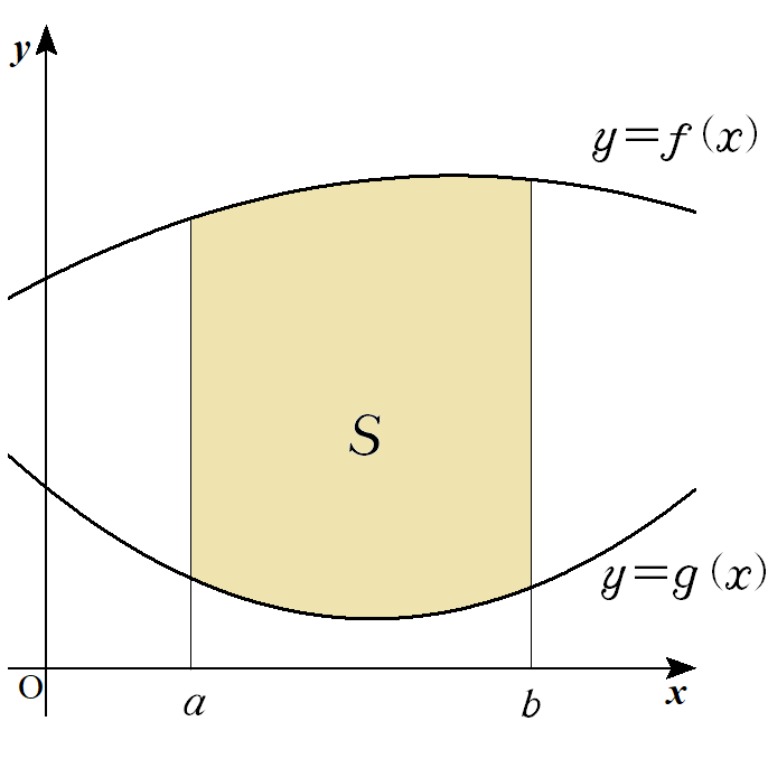
TOSSランド 「いろいろな図形の面積」 (積分) の基礎・基本

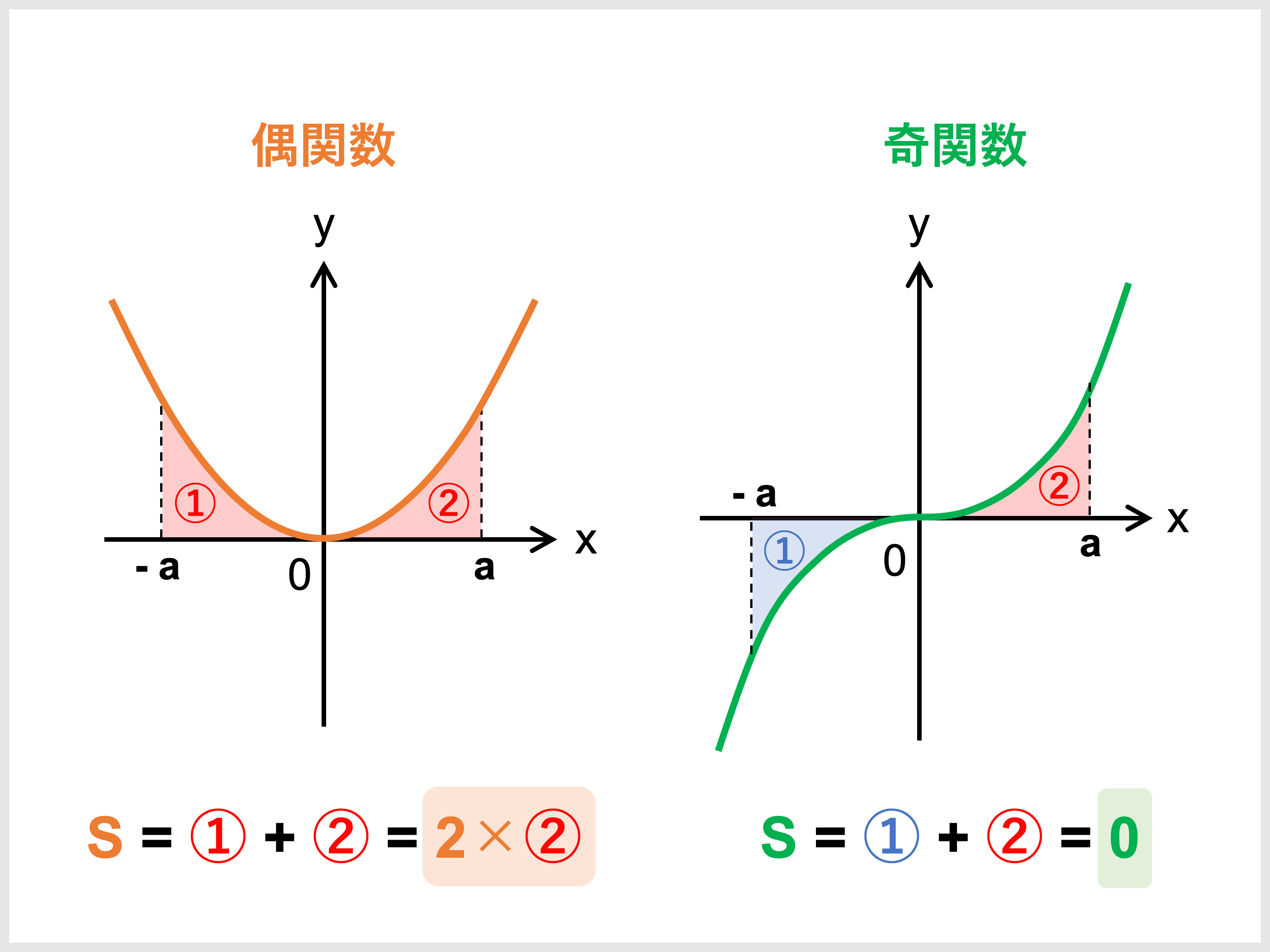
偶関数・奇関数とは？見分け方や定積分の公式を解説！ 受験辞典

定積分と面積

積分計算による体積の求め方！断面積の積分や回転体の体積 受験辞典

重積分を使った曲面積の求め方 YouTube

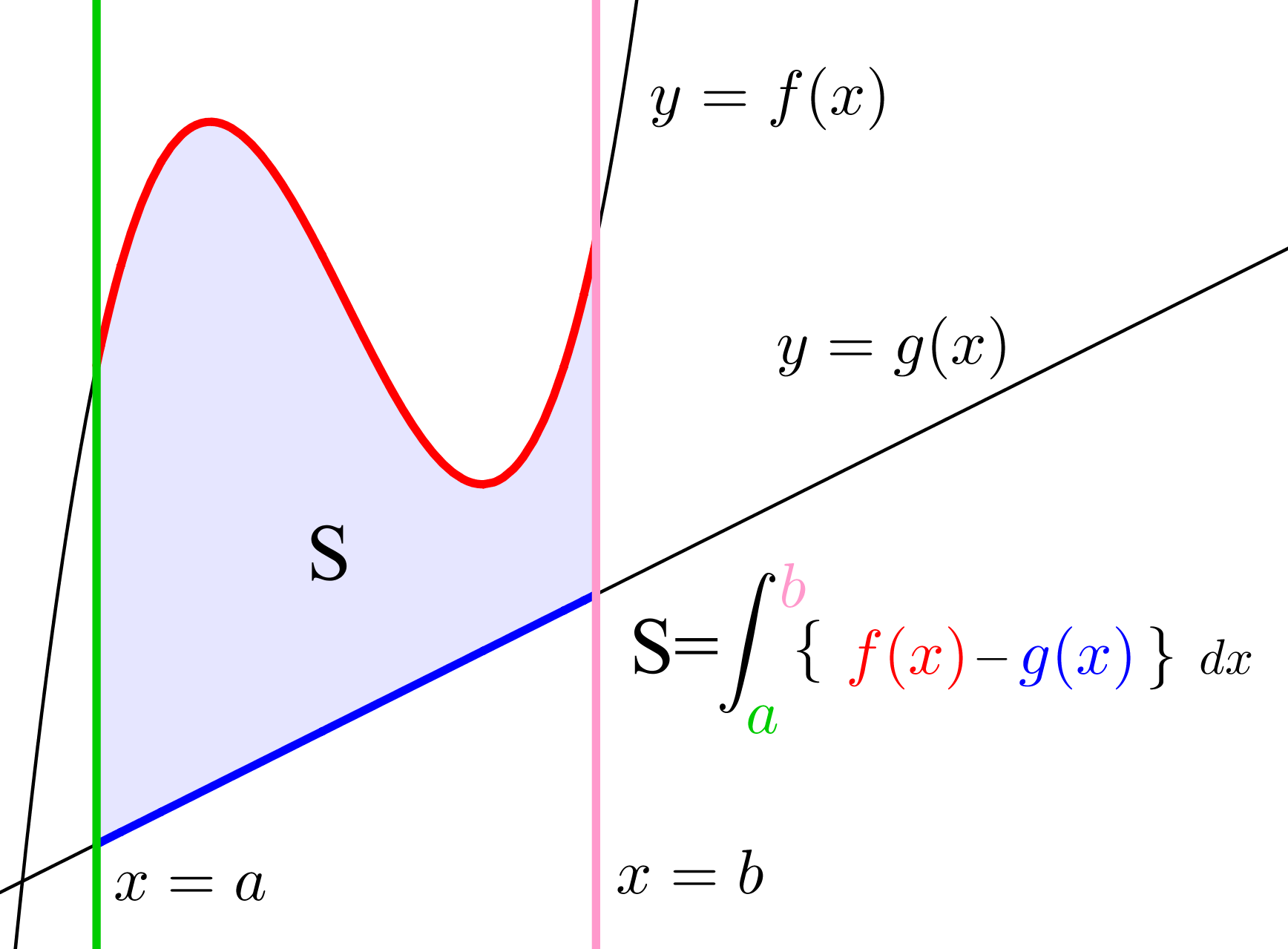
定積分と面積（基本）

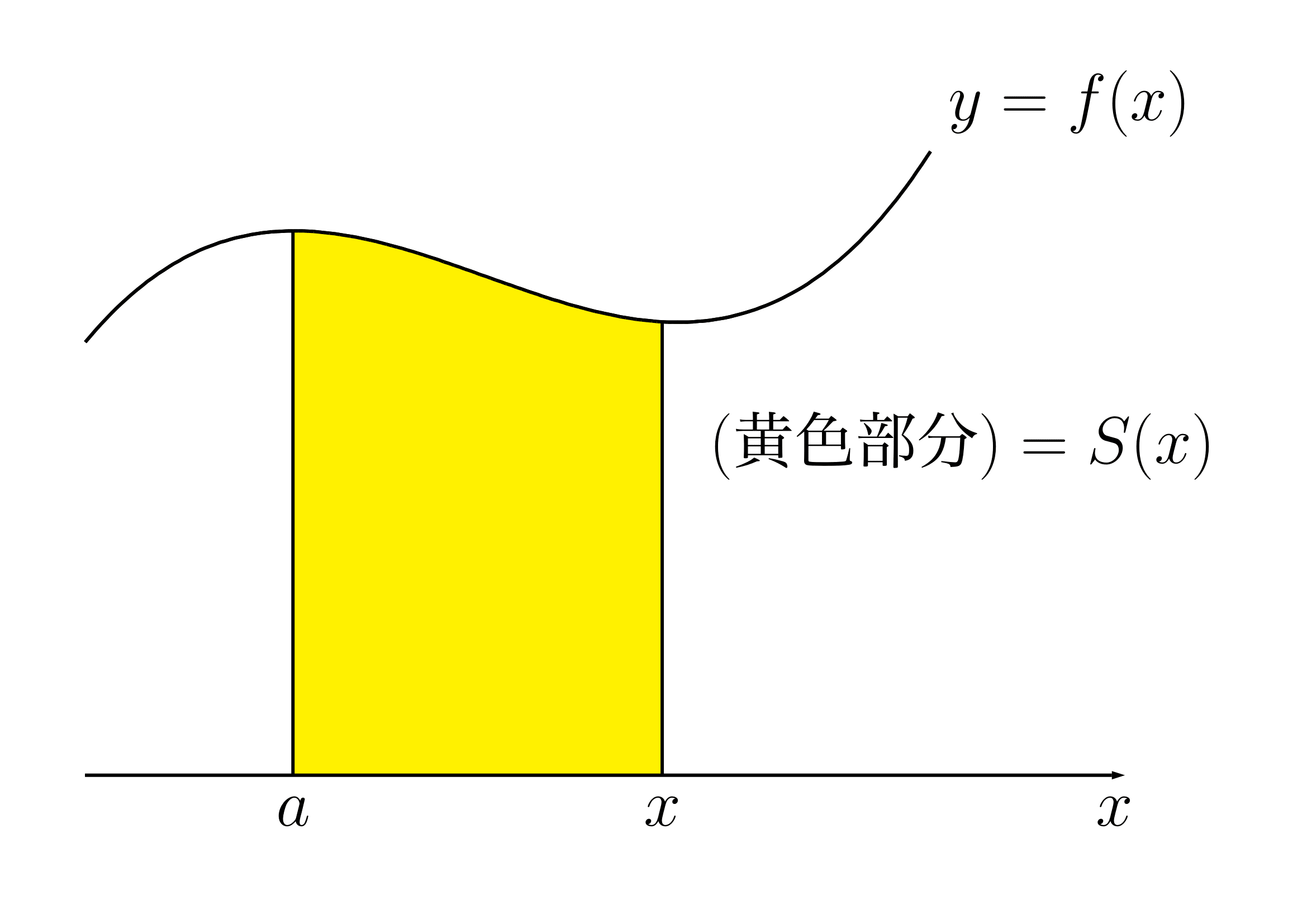
定積分で面積が求まる理由 おいしい数学

定積分の計算手順 すべての知識は積分 やり方に関する最も詳細なものです

グラフ不要！？交点と上下関係だけで求める面積【数Ⅲの積分法が面白いほどわかる】 積分 面積 上下 見分け 方に関連する一般的な文書

数学II 「積分法」 3－3 2曲線間の面積 YouTube

定積分と面積（基本）

このことから y= f(x) y = f ( x) の方が上にあるなら、求める面積は ∫ b a {f(x)−g(x)}dx ∫ a b { f ( x) − g ( x) } d x になるし、 y= g(x) y = g ( x) の方が上にあるなら、求める面積は ∫ b a {g(x)−f(x)}dx ∫ a b { g ( x) − f ( x) } d x なるんだ。. だからどっちの関数が.. まずは図示して求める面積がどの部分かを確認する. このとき,\ 面積を求めるために必要最小限の情報の図を素早く描くことが重要である. 面積を求める時に必要になるのは関数の上下関係や共有点}であり,\ 頂点や極値は必要ない. 多くの面積の問題は,\ 共有点の座標が綺麗な値になるように作成されているはずである. 本問の場合,\ x軸との共有点のx座標は,\ x^2-4=0よりx=±\,2である. 後は定積分すればよいが,\ 本問は上下関係が入れ変わるところで積分区間を分割する}必要がある. x軸の式はy=0なので,\ 正確には∫ {-1} {2}\ {0- (x^2-4)\}\,dx+∫ {2} {3}\ { (x^2-4)-0\}\,dxである.